The paper in full.

Highlighted excerpts:

Finding words for multiplicity

Bergson repeatedly confronted the difficulty that the very means to describe or elucidate his metaphysics seem to run contrary to or betray its essential tenets. In retrospect, one may see the wide disciplinary sweep of Bergson’s writings as in part a reaction to this problem; it is as if he pursued an ongoing search for the linguistic and conceptual ground most appropriate for expressing his philosophical system. Today, thinking through Bergson’s work in the light of contemporary medialities, we may add an additional, retrospective line of speculation. This essay argues that scientific techniques enabled by digital media provide a means of resolving specific difficulties Bergson encountered in trying to translate temporal concepts into language.

“The representation of a multiplicity of “reciprocal penetration,” quite different from numerical multiplicity - the representation of a heterogeneous, qualitative, creative duration - is the point from which I left and where I have constantly returned.”

Bergson’s particular dilemma, we might use his own terms and say that the very act of representing multiplicity in words presents a potential trap, that to do so is to transpose a virtual concept into an actualized symbolic entity.

The short essay “Introduction à la métaphysique,” originally published in 1903, provides a particularly cogent instance of Bergson trying to find the right words to convey his idea that duration is a certain form of multiplicity. This text succinctly summarizes the philosophy developed in Durée et simultanéité and Matière et mémoire. And because it purported to provide a compressed, accessible introduction to his thought and method, this work reveals the crux of Bergson’s struggle with language: on the one hand, he demonstrates his power as a philosophical writer, which rests largely in his ability to convey metaphysical concepts by creating easily comprehensible metaphors or analogies; on the other hand though, each explanatory figure he uses fails in some way, forcing him ultimately to locate the true nature of duration just beyond the reach of language. It is in the very gaps where these shortcomings reside that our retrospective reading of Bergson and medialities begins its work.

Metaphysics must struggle to adhere to an asignifying stream of thought, which does not differentiate its proper object (duration as continuous multiplicity) by projecting it onto discrete symbols. Thus while science re-presents its objects of study in mathematical terms and spatial models, Bergson argues, metaphysics will be founded on an immediate apprehension of its objects of thought from within. It will generate intuitive knowledge based on a “sympathy” with its object rather than “analysis” of the whole in terms of its parts.

“Certainly concepts are indispensable [to metaphysics], because all the other sciences work most commonly on concepts, and metaphysics can not do without other sciences, but it is itself only when it exceeds the concept, or at least when it frees itself from straightforward and ready-made concepts to create concepts very different from those we usually handle, I mean flexible, mobile, almost fluid representations, always ready to be molded on the fleeting forms of intuition.”

Chaos Enters the Picture

I wish to explore a rather simple-sounding thesis: that computer-generated diagrams used in chaos theory provide symbolic tools adequate for expressing specific aspects of the concepts Bergson struggles to articulate in his writing.

As is well known by now, “chaotically” usually means not completely random or all-over-the-place, but a combination of local unpredictability and some form of global order. It used to be that if a system did not behave according to the laws of classical dynamics (where position and momentum of the variables yielded a picture of the system’s evolution), knowledge of it was limited to being statistical. The evolution of a system driven by “chaos dynamics” lies halfway between the stable, predictable trajectories of a classical dynamical system and the random behavior of a system like molecules colliding in a gas. One scenario of how a dynamical system evolves is that it starts out from an initial condition, follows a trajectory within a certain region of its possible behaviors, comes to a fork in its road (a bifurcation point), and, depending on very slight differences, will follow one path or another, and go roaming around the next relatively well defined region for a while, until the next fork comes along.

From the onset of its popularity in the 1980’s, chaos theory exerted a strong aesthetic and philosophical appeal, in large part because of the very nature of what I will refer to as ‘chaos diagrams’—the graphic representations of mathematical models of chaos. Fractal art exhibitions, fractal calendars, software programs all brought art and science together in some way. Simultaneously, scientists instrumental in popularizing chaos theory discussed its philosophical and historical implications, sometimes rather freely. For some, the fact that science was studying nonlinear systems and chaos held out the promise that western science was exploring realms and patterns it had hitherto ignored or excluded. For others, it was as if the interest of science were undergoing a philosophical inflection.

Diagrams: Mathematics, Science and Philosophy

We can find in chaos diagrams a sort of double coding: on the one hand, visual displays which often cannot be immediately correlated with a referent or whose ‘real meaning’ is not easily understood; on the other hand, visual displays which represent mathematics as a process of material construction rather than rarefied manipulation of transparent symbols. Taken together these characteristics enable chaos diagrams to be used as heuristic devices which ‘embody’ some set of relations, without regard to actual content. When I propose specific chaos diagrams as resolutions to dilemmas which arise in Bergson’s philosophical discourse, the diagrams serve as precisely this kind of conceptual algorithm; they provide a means of condensing some complex set of relationships into an abstract configuration. In other words, as diagrams begin to function as philosophical signs, they become energized with a certain potential. Their power rests in the range of their potential uses or meanings; they designate some set of relations which could be obtained in any number of specific contexts. This way of conceptualizing and mobilizing diagrams is an important part of Deleuze’s philosophical method, in that one of his main interests is to disclose homologous patterns and dynamics which underlie processes in disparate domains of the social and physical worlds. Deleuze thus deploys the term diagram in an abstract sense. For Deleuze, a “diagram” is not a static schema or a sketch designed to map the internal relations in a system or whole, but a compressed expression of an insight or intuition that has not yet been given explicit form. In other words, a diagram enfolds a set of relations that must be unfolded in order to be subject to interpretation. […] The diagram therefore expresses virtual relations; it operates on a conceptual rather than representational plane.

If we follow Massumi’s assertions that a diagram designates an encounter, a set of relations between entities, and that a diagram does not crystallize a stable idea, for it persists in “a process of becoming,”8 then diagramming duration itself becomes a self-similar procedure where duration, whose very nature is becoming, gets expressed with conceptual tools that themselves embody becoming.

Diagramming Duration

In essence, we find that Bergson lacks any notion of “space” or spatial metaphors which would accommodate the definitive characteristics of his concept of multiplicity. The chief impasse lies in that fact that qualitative or continuous multiplicity entails “reciprocal penetration,” a tangled weave of sorts, and Bergson could not find a visual or spatial analogue because he equated space in general with the Euclidean space of common sense. Quite simply, the main reason that chaos diagrams serve as such effective heuristic supplements for Bergson’s metaphors for multiplicity is that they are constructed in fractional dimensional spaces where successive magnifications reveal “reciprocal penetration” across different scales. As I proceed now to match one Bergsonian metaphor after another to a particular chaos diagram, the interpretation will no doubt seem rather mechanistic, and my treatment of chaos diagrams rather superficial. But this is only an initial examination of ways to map a conceptual space common to Bergson and chaos theory; the discussion turns from a plane of representation (verbal metaphors matched to visual diagrams) to conceptualization (the relational structure underlying the discourses). One reason to let the discussion unfold this way is that it enacts the process most frequently followed in interdisciplinary thinking: to move from an initial insight of some general analogy between two objects of study to a fuller discussion of where the analogy can take us, where the differences lie, etc.

The Ball of Thread

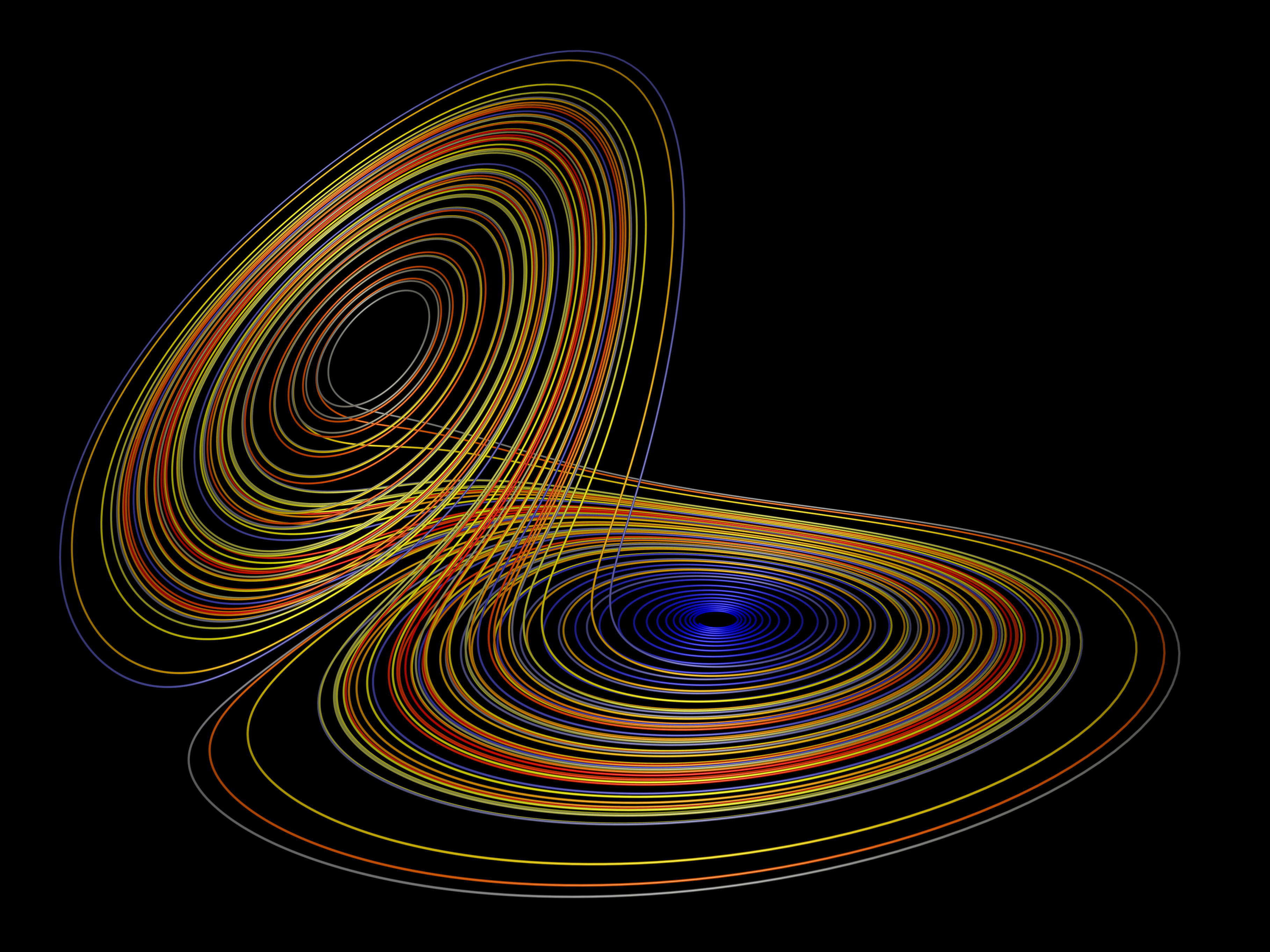
But it is possible to imagine the images of uncoiling thread and thread rolling up onto a ball within a single representation, for this is what characterizes the chaos diagram known as a Lorentz attractor (fig. 1). This image has become a familiar trademark of computer graphics: two disk-like configurations that resemble the grooves on a record, intertwined by trajectories that cross over from one to the other. The rotational motions run in different directions on each one, providing an apt—if rather literal—analogy for Bergson’s “unrolling” and “rolling up” threads. But the Lorentz attractor works as a fitting figure for Bergson’s two thread metaphors at a more conceptual level as well. Bergson employs the image of an unrolling thread as a figure for the span of a person’s inner life, a time-line distinguished in Bergson’s thought by its unpredictability, its openness to choice. This thread of Bergson’s thought finds its equivalent in the Lorentz attractor in the paths of trajectories, which are locally unpredictable and never overlap with one another. Bergson’s image of the rolling up of the thread onto a ball, on the other hand, stands for the qualitative identity that accumulates in a person’s life, the constraint that memory places on the unfolding present of duration. This thread is expressed on the Lorentz attractor as the forming of the composite figure, the attractor to whose general outline the trajectories adhere on a global scale. The attractor evolves as an increasingly enfolded mesh of paths that never cross, because they embed themselves in a fractional-dimension figure.

Thus while Bergson discarded the threads and ball figure because it involved a “homogeneous” space in which lines and surfaces were “superposable on one another,” the enmeshed tangle of the attractor forms a mottled texture of irreducible heterogeneity—there is no way to contract the attractor. It is a heuristic convenience that the fractional dimension of this attractor is between two and three dimensions, for it provides a space that we could imagine as the result of collapsing the two-dimensional threads and the three-dimensional ball. In fact, Mandelbrot uses a ball of thread as an example of how the dimensionality of an object depends on point of view and scale of measure, and then proceeds from there to introduce the idea of fractional dimensions.

Drawing the Line

This seemingly simple distinction invokes Bergson’s crucial differentiation between movement itself, and the space that movement traverses. The “action” of the line being traced, the tracing itself, is a continuous, “indivisible” action; but if we think of it as a line, it becomes a stationary segment and thus can be broken into smaller “cuts.” This distinction was the basis for Bergson’s answer to Zeno’s paradoxes, which are founded on the translation from continuous movement to discrete steps. Bergson concludes by stipulating that if we wish to correlate movement and duration, “finally, let us free ourselves from the space that underlies the movement to take into account only the movement itself, the act of tension or extension, and finally pure mobility.” Bergson’s distinction between movement and its representation as a trajectory in space is immensely important in this context. Bergson’s philosophical distinction may be understood in relation to the classical dynamical models of his day. The dominant model, first formulated by Lagrange in 1788, depicts motion not as a primary event but as an effect, a kind of epiphenomenon. This model derives motion from static representations of spatial and temporal position. Thus motion remains chained to the rate of change of position; in both a technical and figurative sense, motion is a derivative of position. When Bergson demands that we free motion from the space it occupies, he reverses this dependence of movement on position: he places motion prior to change of position, making it impossible to think of motion as a sequence of dimensionless points threaded together.

Chaos diagrams are composed in a way that trace a way out of the dilemma in which Bergson’s metaphors place him. First, chaos dynamics differs crucially from classical dynamics in that space no longer precedes movement in the same way. A chaotic motion or “orbit” does not occupy a fixed, box-like space; it rather outlines the space needed to hold it as it unfolds; it produces its own spatial form as it evolves. Deleuze and Guattari conceptualize this kind of diagramming in terms of “smooth space” (espace lisse). […] Similarly, an orbit of a system in phase space is not a trajectory through a Euclidean box of length, width and depth; dimensions of phase space represent variables of the system, so an orbit does not represent a system’s motion in space, but “a map of the changes in the system’s behavior over repeated cycles.”

If Bergson’s image is diagrammed using tools from chaos theory, it would unfold as follows. The body contracted to a point, from which a line extends out, becomes a tangled mesh, a spreading shape of constant volume that occupies more and more of a multi-dimensional phase space. What Bergson imagined as a linear trajectory “in” space (which he then had to extract from the space) gives way to a fractal-dimensional, shifting form that creates the space it occupies. Prigogine and Stengers’s description of how to diagram the evolution of an unstable system redraws Bergson’s image on a chaos graph very neatly:

Suppose that our knowledge of initial conditions permits us to localize a system in a small cell of the phase space. During its evolution, we shall see this initial cell twist and turn and, like an amoeba, send out “pseudopods” in all directions, spreading out in increasingly thinner and ever more twisted filaments until it finally invades the whole space.

Continuous Multiplicity

Picking up the passage from “Introduction à la métaphysique”, Bergson drops the contracted point metaphor for duration because while it expresses the “simple movement through which consciousness passes from one nuance to another,” this simple movement depicted as a smooth line fails to express the heterogeneity of duration, its continual differing from itself. For Bergson, the insurmountable difficulty in finding the proper conceptual figure for duration is that no image can represent duration as both continuous with itself and differing from itself. Duration cannot be rendered in a single figure of language or thought because it “in some respects resembles the unity of a movement that is progressing, by others to a multiplicity of spreading states, and that no metaphor can render one of the two aspects without sacrificing the other.” Bergson is thus left simply to contain the problem in a paradoxical — for him perhaps oxymoronic—formulation. The continuous “unity of advancing movement” and its irreducible “multiplicity” of content leave Bergson to posit that duration is a continuous multiplicity, even if he must admit that: “if there is a multiplicity […], this multiplicity is unlike any other.” Thus while Bergson maintains that duration is a consistent philosophical concept, in his rhetorical turnings duration is figured as a concept split into two seemingly contradictory components. The self’s “inner life” as both “the unity of an advancing movement” (“unité d’un mouvement qui progresse”) and “the multiplicity of expanding states” (“multiplicité d’états qui s’étalent”) cannot be grasped in a single image; “no metaphor can render one of the two aspects without sacrificing the other.”

The Knead for Chaos

We now bring the diagramming of duration to a close with a final set of connections between Bergson’s metaphysics and chaos theory. The basic line of thought here runs as follows: fractal attractors may be mobilized as diagrams for duration because they exemplify and help conceptualize its structural principles, the primary one of which is a double movement of horizontal unfolding and vertical recoil or rotation.

At the formative level of duration, there are two “simultaneous movements” which weave together somehow without ever being superposable or homogeneous strands. These two movements traverse sides of what becomes a fold.

In an essay published in Scientific American that helped popularize chaos, members of the Santa Cruz Dynamical Systems Collective describe this metaphor succinctly:

The key to understanding chaotic behavior lies in understanding a simple stretching and folding operation, which takes place in the state space. Exponential divergence is a local feature: because attractors have finite size, two orbits on a chaotic attractor cannot diverge exponentially forever. Consequently, the attractor must fold over itself. […] The process of stretching and folding happens repeatedly, creating folds within folds ad infinitum. A chaotic attractor is, in other words, a fractal: an object that reveals more detail as it is increasingly magnified.

The conceptual link between duration as continuous multiplicity and fractals finds its mathematical analogue expression in the fact that Riemann’s continuous multiplicities are a class of fractals.

An apt formulation of the matter would be that chaos diagrams are actual representations of virtual multiplicities.

In this sense, the fractal maps onto the discussion of Bergson’s descriptions of how the past gathers itself and folds into the present, that is, this folding cannot be reduced to a single heuristic metaphor or image, but must be figured as a process of continual remixture and redistribution. The fractal as actual object, we might say, has a presence in the present only as a virtual fissuring. Apprehended this way, the fractal functions not as an ideal object outside thought, but a diagram that filters thought into a mobile form. The fractal enacts or even embodies, stands in for, a fundamental duplicity which lurks at the very heart of “time” as a conceptual entity.

Here, in a strictly metaphorical sense, we may borrow one more figure from chaos theory to diagram the form this metaphysical knowledge takes in our topological cerebral space. The Poincaré surface-of-section is a method used to study the properties of an attractor (fig. below). Because the attractor is a thickly braided, impossibly entangled weave of trajectories, one cannot ever have an “objective” view of it. Instead, the Poincaré surface-of-section extracts a pattern by cutting a perpendicular slice of the attractor, producing a set of points that represent where the attractor passes through the plane. This set of points allows certain qualitative assessments to be made about the attractor, but does not yield any predictive or quantitative results. The heuristic power of the figure in this context lies in the fact that the surface-of-section is a lower-dimensional view, a procedure performed immanent to the whole; yet its pattern allows qualitative inferences and distinctions to be made about the nature of the system’s behavior. This image of thought precludes the fixity of the concept, its exteriority to the object of its discourse. Instead, it is like a route through smooth space, where the route maps out its own space by proceeding.

The Poincare section.